Masa Resorte

 

Cómo analizar sistemas masas-resorte verticales y horizontales

Los sistemas masa-resorte sin fricción verticales y horizontales oscilan de forma idéntica alrededor de una posición de equilibrio si sus masas y resortes son iguales.

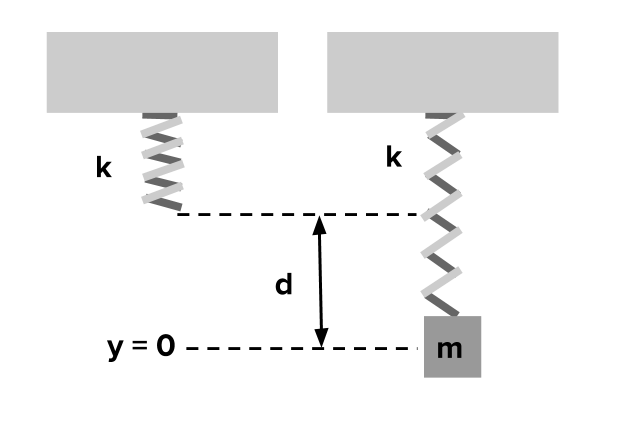
Sin embargo, en los resortes verticales, debemos recordar que la gravedad estira o comprime el resorte más allá de su longitud natural desde la posición de equilibrio. Después de encontrar la posición de desplazamiento, podemos establecerla como el punto donde $y=0$y, equals, 0 y tratar el resorte vertical tal como lo haríamos con un resorte horizontal. La Figura 1 a continuación muestra la posición de reposo de un resorte vertical y la posición de equilibrio del sistema resorte-masa después de que se ha estirado una distancia $d$d.

Figura 1. A la izquierda de esta imagen está la posición en equilibrio del resorte y a la derecha está la posición del desplazamiento del resorte a partir del equilibrio cuando se une a la masa. Un sistema vertical masa-resorte oscila alrededor de esta posición de equilibrio de $y=0$y, equals, 0

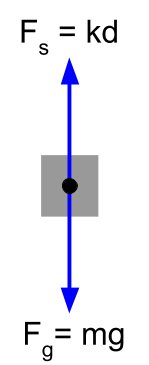
Podemos usar un diagrama de cuerpo libre para analizar el movimiento vertical de un sistema masa-resorte. Representamos las fuerzas sobre el bloque de la Figura 1 como sigue:

Figura 2. Las fuerzas en el sistema masa-resorte de la Figura 1

Luego, podemos usar la segunda ley de Newton para escribir una ecuación para la fuerza neta sobre el bloque:

$\begin{aligned}\Sigma F &= ma \\ \\ &=F_s - F_g \\ \\ &= kd - mg \end{aligned}$

El bloque de la Figura 1 no se está acelerando, por lo que nuestra ecuación se simplifica a:

$kd - mg = 0$k, d, minus, m, g, equals, 0

Errores conceptuales comunes

A veces las personas piensan que el periodo de un oscilador masa-resorte depende de la amplitud. Aumentar la amplitud significa que la masa viaja una mayor distancia durante un ciclo. Sin embargo, incrementar la amplitud también aumenta la fuerza de restitución. El aumento en la fuerza incrementa proporcionalmente la aceleración de la masa, por lo que la masa se mueve una mayor distancia en el mismo tiempo. Así que aumentar la amplitud no tiene un efecto neto en el periodo de la oscilación.